선형결합 (인공지능을 위한 선형대수, 20210422)

선형대수에 대한 이해를 돕기 위해 edwith의 인공지능을 위한 선형대수 수업을 듣고 작성한 복기내용입니다.

 

선형대수에서 선형결합이란, p개의 벡터가 주어져 있을 때 p개의 상수배를 하여 더해주는 형태를 말한다.

그리고 아래와 같이 3차원에 존재하는 행렬 $A$를 각각의 컬럼벡터 $a_1, a_2, a_3$로 정의하고 $a_1x_1 + a_2x_2 + a_3x_3 = b$로 변환시킬 수 있다. 이런 형태를 벡터 방정식이라고 부른다.

이를 통해 이 방정식의 Solution(해)이 있는지 없는지를 따지는 기준으로 활용할 수 있다.

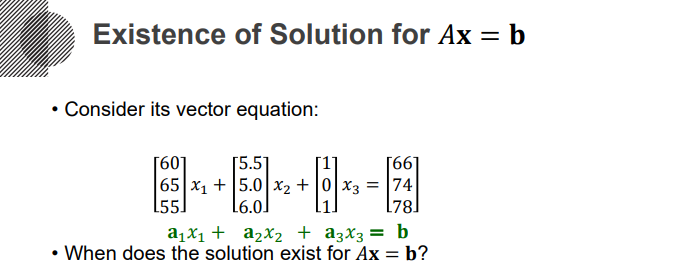
이를 위해서는 먼저 Span이라는 개념을 이해할 필요가 있다. 만약 재료벡터(v)가 p개있고, p차원 공간에 있다고 가정하자. 그리고 이 재료벡터들에 대해 사용할 수 있는 계수 혹은 가중치(c)들로 쓸 수 있는 값들을 다양하게 적용해본다. 그리고 이런 모든 조합의 계수들을 써서 만든 결과벡터들을 모은 것이 Span이다. 이 Span에 대해서 시각적인 이해을 원한다면 아래의 영상이 도움이 될 것이다.

  그렇다면 이 Span이라는 것이 기하학적으로, 공간적으로 어떤 의미를 가지는지 알아보자. 먼저 아래와 같이 2개의 재료벡터 $v_1, v_2$가 있다. $v1 = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}, v2 = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}$이다. 먼저 $v_1$에 1상수배를 하고 $v_2$에 1상수배를 한(선형결합한) 값은 \begin{bmatrix} 5 \\ 7 \\ 9 \end{bmatrix}이다.  혹은 $v_1$에 -3상수배를 할 수도 있을 것이다. 이런 모든 경우의 수에 대한 선형결합의 결과값을 모았을 때 만들어지는 집합은, 재료 벡터 $v_1, v_2$에 대해 가능한 모든 선형결합의 결과라는 것을 알 수 있다. 이것이 Span이다. 아래의 설명을 들어 말하자면, 유한한 개수의 벡터 $v_1$과 $v_2$가 3차원 공간상에 존재했을 때 이 두 벡터로 만들 수 있는 모든 선형결합을 모아놓은 벡터들의 부분집합이 Span이다.

 

  그럼 이런 의문이 생길 수 있다. 만약, 3차원 공간 안에 3개의 재료 벡터가 존재한다면 어떻게 될까? 그렇다면 Span의 집합은 평면이 아닌, 3차원 모든 공간을 차지할 것이다 즉 Span은 3차원 공간의 전체집합이 된다. 똑같은 논리로 4차원 공간 안에 3개의 재료 벡터가 존재한다면, 벡터는 4차원 안에 존재하지만 이 벡터들의 Span은 4차원 공간 안의 부분집합(3차원)이 될 것이다.

다시 본론으로 돌아와서, 우리는 $A\mathbb{x} = b$라는 식에 해가 존재할 것이냐 하지 않을 것이냐에 대해서 이야기하고 있었다. 이것에 대한 설명은 $a_1, a_2, a_3$벡터의 선형결합의 집합인 Span안에 벡터 $b$가 존재한다면 해는 존재하게 되며 그렇지 않으면 해가 없게 된다고 설명할 수 있다.

다음으로는 행렬의 곱을 이해하는 4가지의 시각을 알아보도록 한다.

  첫 번째로, 원래 행렬곱이라고 하면 e.g.에 나온 것 처럼 3 * 1 + 4 * 2 처럼 내적을 하게 되는데 이 행위를 총 6번 하게 된다. 이것을 [ 60, 65 55 ] , [ 5.5 5.0 6.0 ] , [ 1, 0, 1 ]( a1, a2, a3 )의 3개의 컬럼벡터와 [ x1, x2, x3 ]의 가중치 벡터의 선형결합으로 표현할 수 있다. 

(아래)이렇게 [ 1, 1, 1 ], [ 1, 0, -1 ], [ 0, 1, 1 ] 3개의 컬럼벡터에 [ 1, 2, 3 ]의 가중치를 선형결합하여 표현하는 것처럼 말이다. 하지만 이런 방법은 일반적인 행렬곱은 아니다. 왜냐하면 [ 1, 2, 3 ]은 행렬이 아니라 벡터이기 때문이다. 그렇다면 행렬 * 행렬의 관계에서도 이렇게 표현할 수 있을지에 대한 의문이 남는다.

  Multi-columns on the right를 보자. 가중치가 행렬로 표현이 될 때는 x와 y에 대한 3x2행렬이 나오게 된다. 이 3x2 행렬 ( x1 x2, x3과 y1, y2, y3이 있는 )을 따로따로 생각해볼 수 있다. 첫 번째 컬럼 벡터는 x 두 번째 컬럼 벡터를 y라고 생각하면 x는 왼쪽 행렬과 오른쪽 첫 번째 컬럼 벡터( [ 1, 2, 3 ] )의 선형결합, y는 왼쪽 행렬과 오른쪽 행렬의 두 번째 컬럼 벡터( [ -1, 0, 1 ] )의 선형결합으로 각각 표현할 수 있다. 똑같은 왼쪽 행렬(3개의 컬럼 벡터)에 대해 [ 1, 2, 3 ]의 가중치를 선형결합한 x와 [ -1, 0, 1 ]에 대해 선형결합한 y가 나오게 된다. 

두 번째로는 row 벡터의 combination ( 선형결합 )을 생각해 볼 수 있다. 위에 있던 행렬식을 Ax였다고 생각해보자. 이 값을 Transpose하게 되면 x^-1*A^-1이 된다. 이 식이 밑에서(One row on the left)에서 볼 수 있는 [ 1, 2, 3 ]의 row 벡터와 행렬의 row 벡터와의 곱이다. 여기서는 위에서 봤던 가중치( 컬럼 벡터 )[ 1, 2, 3 ]는 로우 벡터로 변환된다. 그리고 오른쪽 재료 벡터들을 row 벡터 형태로 선형결합한 형태와 동일한 것을 확인할 수 있다.

세 번째로는 [ 1, 1, 1 ]의 column벡터와 [ 1, 2, 3 ]의 row벡터를 하나의 a, b로 보는 것이다. column벡터와 row벡터의 곱은 외적(outer products)이다. 그리고 [a], [b]에 각각 c, d를 넣어준다. 그렇게 되면 row 벡터 [ a, c ]와 column 벡터 [ b, d ]가 되며 행렬곱을 하게 되면 ab+cd라는 내적값을 얻을 수 있다. 이 말은, a와 b에 대한 outer product 그리고 c와 d에 대한 outer product를 각각 진행한다는 뜻이며, 이렇게 각각 outer product를 진행한 후에 결과값들을 더하게 되면 이것이 행렬곱과 같다라는 것이 세 번째 행렬곱을 바라보는 시각이다.